Předmět: Pravděpodobnostní modely (KEM/PMO)
Zadání: Vypracovat seminární práci na téma Teorie zásob – Model s konstantní velikostí dodávky při poklesu zásoby na signální hladinu. Sestavte příklad a vypočítejte optimální velikost dodávky.
Autor: Roman Sterly
Datum: 19. 6. 2011
Obsah
- Zadání seminární práce
- Zásoby
- Členění zásob
- Modely zásob
- Deterministický dynamický model zásob s konstantní velikostí dodávky
- Stochastický dynamický model zásob s konstantní velikostí dodávky
- Použitá literatura
Zadání seminární práce
Úloha č. 18: Teorie zásob – model s konstantní velikostí dodávky při poklesu zásoby na signální hladinu, sestavte příklad a vypočítejte optimální velikost dodávky.
Zásoby
Zásobami se v podnicích označují suroviny, materiál, polotovary nebo hotové výrobky, které tyto podniky vlastní, nebo budou vlastnit. Jejich funkcí je vyrovnat časový nesoulad mezi výrobou a spotřebou.
Lukáš zásoby definuje jako „… okamžitě použitelný zdroj, který je systematicky vytvářen k materiálovému zabezpečení plynulého průběhu výrobního procesu, či uspokojení poptávky na trhu.“ (Lukáš, 2005)
Z ekonomického pohledu představují zásoby náklady, neboť zdroje, které někde leží, mohly jinde pracovat. V tomto případě se tedy jedná o náklady ztracených příležitostí. Na rozdíl od ekonomických nákladů spojených s pouhým držením zásob, vznikají účetní náklady až v době skutečné spotřeby zásob. Dále můžeme do nákladů, které se zásobami souvisejí, zahrnout náklady na objednávání, držení a jejich kontrolu.
Z těchto důvodu je v moderní době dbán důraz na snižování zásob a tedy redukci nákladů pomocí štíhlejší výroby, prosazují se principy Just in Time. Strategie držení zásob Just in Time je taková, která se snaží o zvýšení rentability efektivní výrobou a zamezení plýtváním prostředků firmy.
Členění zásob
Zásoby lze členit podle mnoha hledisek. Příkladem může být členění podle funkcí, podle disponibility, podle použitelnosti nebo podle jejich stavu.
Podle funkcí můžeme zásoby členit na:
- Obratová zásoba – pro krytí potřeby výroby mezi dvěma dodávkami zásob
- Pojistná zásoba – pro krytí náhodných výkyvů ve výrobě
- Zásoba pro předzásobení – pro potřeby v případě sezónnosti
- Strategická zásoba – pro zvýšení jistoty v případě nepředvídaných událostí
- Spekulativní zásoba – pro využití určité příležitosti – např. při očekávaném zvýšení cen zásob
- Technologická zásoba – pro potřeby technologického postupu výroby
Podle stavu zásob můžeme zásoby členit na:
- Maximální zásoba
- Minimální zásoba
- Průměrná zásoba
Modely zásob
Smyslem modelů zásob je vyřešit, kdy objednat dodávku nových zásob a jak velká by objednávka měla být. Dvě extrémní situace mohou být
- Velmi vysoký stav zásob, který sice zajišťuje plynulou výrobu mezi dvěma dodávkami, ale zároveň s sebou nese vysoké skladovací náklady
- Velmi nízký stav zásob, který sice minimalizuje skladovací náklady, ale nezajišťuje plynulou výrobu
Základními prvky, kterými by se měl management při řízení zásob zabývat, jsou:
- Jak funguje sklad zásob zboží – máme jeden produkt, nebo více produktů; probíhá čerpání zásob periodicky, nebo neperiodicky
- Jak je sklad doplňován – okamžitě, náhodně, postupně, dochází k prodlevám
- Jak je zboží ze skladu odebíráno – náhodně, nebo deterministicky
- Dochází na skladu k nějakým ztrátám
- Existují nějaká omezení – velikost skladu, financování
Modely teorie zásob lze členit podle různých hledisek. Existují modely statické a dynamické. V případě statického modelu zásobse jedná o jedinou dodávku, která když se jednou pořídí, nemůže už být znovu doplněna. Z této zásoby je poté uspokojována potřeba podniku. Pokud je zásoba nedostatečná, vznikají náklady z jejího nedostatku. Naopak při vyšší zásobě vznikají náklady související se zbytkovým množstvím po skončení období.
V případě dynamického modelu zásob je možné sklad v čase doplňovat. Dále rozlišujeme, jestli lze proces objednávání zásob v čase měnit. V průběhu procesu se sleduje hladina zásob na skladě a to buď kontinuálně, nebo ve vymezených časových intervalech.
Dále můžeme modely rozlišit na deterministický a stochastický. Dynamický deterministický model zásob předpokládá, že poptávka je v průběhu času určena deterministicky, tzn. Je dána známou funkcí x(t) definovanou na T. Na druhou stranu stochastický dynamický model zásob předpokládá poptávku vyjádřenou náhodně veličinou X, neboli stochastický proces X(t) definovaný na T. Ve většině případů předpokládáme, že poptávka je stanovena pro celé řešené období.
Deterministický dynamický model zásob s konstantní velikostí dodávky
Model zásob s konstantní velikostí dodávky je dynamický a deterministický, obsahuje jeden výrobek a další předpoklady.
Model EOQ (economic order quantity)
Zdroj: http://www.marcbowles.com
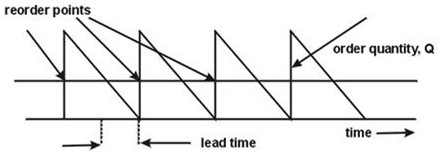
Model EOQ je základním a nejznámějším modelem, kde je spojitá poptávka a v čase se nemění. V literatuře můžeme najít i označení Harrisův-Wilsonův model.
Zásoby jsou v tomto modelu objednávány o stejné velikosti. Po jejich pořízení roste jejich hladina do maxima, ze kterého postupně klesá. V určitém čase je potřeba objednat další zásoby tak, aby přišly na sklad včas.
Náklady na pořízení zásob zahrnují výběr dodavatele, uskutečnění objednávky, dopravu, převzetí na sklad, kontrolu objednávky, atd. V modelu se tyto náklady stanovují vzhledem k počtu objednávek. Náklady na skladování zahrnují práci skladníků, údržbu skladu a jejich provoz, nájemné, apod. Stanovují se většinou vzhledem k průměrné výši zásob na skladě.
Při výpočtech se v modelu řeší počet dodávek, celkové náklady na pořízení zásob, celkové náklady na skladování zásob, celkové náklady strategie řízení skladu. Optimalizovat můžeme velikost dodávek, jejich počet a délku dodávkového cyklu, a signální hladinu zásob s cílem minimalizovat celkové náklady.
Kromě modelů zásob EOQ se můžeme setkat s modely POQ, jde o model periodicky doplňovaných zásob, kde je rychlost doplňování konečná, nebo různými modifikacemi a variantami obou výše zmíněných modelů (uvažování opčního nebo diferenciálního rabatu, možnost přechodného nedostatku, víceproduktové modely, atd.).
Na následujícím příkladu jsou ukázány obecné formulace příslušných vzorců a dále jejich aplikace.
EOQ model – vlastní příklad
- Firma za rok prodá 60000 výrobků
- Doplňování skladu probíhá 2x měsíčně
- Objednává se dodávka 2500 výrobků
- Pořizovací cena jednoho výrobku je 100 Kč
- Poptávka po výrobcích je během roku rovnoměrná.
- Roční skladovací náklady 1 výrobku jsou 15% pořizovací ceny
- Náklady na dodávku do skladu jsou 1000 Kč, přičemž velikost dodávky nehraje vliv
- Během roku uvažujeme 250 pracovních dní
- Pro délku pořizovací lhůty řešíme dva případy
- Pořizovací lhůta je 10 dní
- Pořizovací lhůta je 14 dní
Stanovíme:
- Celkové náklady strategie řízení skladu
- Optimální velikost dodávky
- Minimální celkové náklady
- Optimální počet dodávek a délku dodávkového cyklu při optimálních dodávkách
- Signální úroveň zásoby v obou zadaných případech
Použité veličiny
| D | spotřeba výrobků za jednotku času |
| d | spotřeba na časovou jednotku |
| Q | velikost dodávky na sklad |
| N(Q) | nákladová funkce |
| Np(Q) | náklady na pořízení dodávky |
| Ns(Q) | náklady na skladování dodávky |
| ns | náklady na skladování 1 výrobku za jednotku času |
| np | náklady na pořízení 1 dodávky |
| T | délka dodávkového cyklu |
| P | počet dodávek |
| p | pořizovací lhůta |
| y | počet pracovních dní v roce |
| S | signální úroveň zásob |
| w | dodávky na cestě |
Celkové náklady strategie řízení skladu
Obecně: N(Q) = Ns(Q) + Np(Q) = ns * (Q/2) + np * (D/Q)
Příklad: N(Q) = 100 * 0,15 * 2500/2 + 1000 * 60000/2500 = 42750 Kč
Optimální velikost dodávky
Obecně: Q(opt) = ((2 * np * D)/ns) ^ (1/2)
Příklad: Q(opt) = ((2 * 1000 * 60000)/(100*0,15)) ^ (1/2) = 2829 ks
Minimální celkové náklady
Obecně: N(Q(opt)) = (2 * np * ns * D) ^ (1/2)
Příklad: N(Q(opt)) = = 42426,4 Kč
Optimální počet dodávek
Obecně: P(opt) = D/Q(opt)
Příklad: P(opt) = 60000/2829 = 21,2 dodávek
Délka dodávkového cyklu
Obecně: T(opt) = Q(opt)/D = ((np * 2) / (D * ns)) ^ (1/2)
Příklad: T(opt) = ((1000 * 2) / (60000 * 100 * 0,15)) ^ (1/2) = 0,0471 roku = 11,785 pracovních dní
Signální úroveň zásoby
Signální hladina – délka pořizovací lhůty 10 dní
Pořizovací lhůta je kratší než dodávkový cyklus:
Obecně: S = D * p / y
Příklad: S = 60000 * 10/250 = 2400 ks
Signální hladina – délka pořizovací lhůty 14 dní
Pořizovací lhůta je delší než dodávkový cyklus – nutné určit počet dodávek na cestě:
Obecně: w = p/T(opt)
Příklad: w = 14/11,785 = 1,2
Vzhledem k tomu, že v okamžiku objednání zásob je 1 dodávka na cestě, je nutné odečíst objem této dodávky od spotřeby zásob v době pořizovací lhůty.
Obecně: S = D * p / y – Q(opt)
Příklad: S = 60000 * 14/250 – 2829 = 531 ks
Závěry
V příkladu s obchodní firmou jsme došli k tomu, že celkové roční náklady strategie řízení skladu činí 42750 Kč, optimální velikost dodávky činí 2829 kusů, minimální celkové náklady jsou 42426 Kč, optimální počet dodávek je 21,2 za rok při délce objednávkového cyklu 11,785 dní. V případě desetidenní pořizovací lhůty je signální hladina 2400 kusů a v případě čtrnáctidenní pořizovací lhůty činí 531 kusů.
Stochastický dynamický model zásob s konstantní velikostí dodávky
Jak již bylo uvedeno výše, dynamický stochastický model má poptávku vyjádřenou jako náhodnou veličinu. Většinou uvažujeme poptávku, která je akumulovaná (agregovaná) za celé období T.
Budeme uvažovat jednoduchý příklad, kdy podnik spotřebovává materiál, který mu je dodáván v dávkách o konstantní velikosti. Spotřeba materiálu, resp. poptávka po produktech, je dána pravděpodobnostně a dochází k náhodným odchylkám od střední hodnoty skutečné spotřeby. Existují dva způsoby, jak lze kolísání poptávky (spotřeby) vyrovnávat. V prvním případě můžeme měnit frekvenci dodávek při jejich konstantní velikosti, ve druhém můžeme měnit velikost dodávek při jejich konstantní frekvenci. Podle toho rozlišujeme dva systémy řízení skladu:
- Q-systém (fixed – order quantity model)
- P-systém (fixed – time period model)
Q – systém zásob tedy pracuje se stále stejnou velikostí objednávaného materiálu a mění frekvenci objednávek. P – systém zásobmá stále stejnou frekvenci objednávek, ale mění jejich velikost.
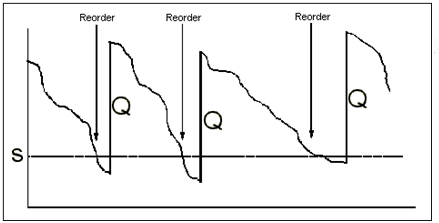
U Q – systému se stanovuje signální hladina zásob, která slouží ke krytí spotřeby během vyřizování objednávky. Jakmile zásoby materiálu na tuto hodnotu klesnou, jsou objednány další.
Zdroj: http://ops.fhwa.dot.gov/
Proti výkyvům ve spotřebě je nutné se zajistit dobře stanovenou signální hladinou. Pojistná zásoba chrání firmu proti důsledkům, které by vyvolala spotřeba během vyřizování objednávky.
Systém je vhodný, pokud je poptávka / spotřeba relativně vyrovnaná a nedochází k příliš velkým výkyvům.
Q – systém model – vlastní příklad
Předpoklady modelu:
- Poptávka je vyjádřena jako agregátní poptávka daná náhodnou veličinou Q s daným rozdělením a střední hodnotou E(Q)>0 a E(Q)<∞ na celkovou dobu řízení skladu T
- K čerpání zásob dochází v jednotlivých cyklech při konstantní rychlosti (rychlost čerpání je v každém cyklu jiná), střední rychlost čerpání je daná na dobu T
- Máme 1 druh zboží
- Materiál je objednán, když průběžná hodnota hladiny zásob poklesne na signální hladinu s
- Objednávka má konstantní objem q
- Během objednání a doručení materiálu, který trvá dobu t(i), se zásoby sníží z hladiny s na hladinu b(i) a ze skladu ubyde množství d(i)
Dále je nutné znát charakter poptávky, který je vyjádřen pomocí pravděpodobnostního rozdělení, jeho střední hodnoty asměrodatné odchylky. V příkladu předpokládáme normální rozdělení N(µ,σ2).
Pro výpočty můžeme použít stejné vzorce jako u deterministického modelu, přičemž namísto deterministické poptávky Q použijeme její střední hodnotu E(Q) = µ.
Řešit budeme:
- Velikost objednávky
- Stanovení pojistné zásoby
- Stanovení signální úrovně zásoby
- Průměrná roční poptávka µ = 60000 výrobků se směrodatnou odchylkou σ = 5000 výrobků
- Pořizovací lhůta dodávky d = 10 dní, v ročním vyjádření 10 / 360 = 1 / 36 roku
- Jednotkové skladovací náklady jsou 15 Kč
- Pořizovací náklady jsou 5000 Kč
Formulace příkladu
Poptávku a její směrodatnou odchylku můžeme vyjádřit:
µ(d) = 60000 / 36 = 1667 ks
σ(d) = 5000 / 36 = 139 ks
Optimální velikost dodávky
Q(opt) = ((2 * 1667 * 5000) / (15 * 1 /36)) ^ (1/2) = 6325 ks
Pojistná úroveň zásoby
Poptávka má během pořizovací doby normální rozdělení N(µ(d),σ(d)) = N(1667,139). Dále budeme předpokládat, že firma bude usilovat o uspokojení poptávky na 90%, nebo na 95%.
w ≥ z0.90 σ(d)= 1,282 * 139 = 178 ks
w ≥ z0.95 σ(d)= 1,645 * 139 = 229 ks
Signální úroveň zásoby
Signální úroveň zásoby budeme uvažovat pro jistotu 95%.
d = 60000 / 360 * 10 = 1667 ks
Optimální úroveň signální hladiny s = 229 + 1667 = 1896 ks.
Závěry
V příkladu s obchodní firmou jsme došli k tomu, že optimální velikost dodávky činí 6325 kusů, pojistná zásoba je 229 kusů a optimální úroveň signální hladiny je 1896 kusů.
Použitá literatura
LUKÁŠ, L., Pravděpodobnostní modely. Plzeň: Západočeská univerzita, 2005
PLEVNÝ, M., Modelování a optimalizace v manažerském rozhodování. Plzeň: Západočeská univerzita, 2010
SLABÁ, K., Teorie zásob. Plzeň: Západočeská univerzita, 2009
JABLONSKÝ, J., Operační výzkum: kvantitativní modely pro ekonomické rozhodování. Praha: Professional Publishing, 2007
PERNICA, P., Logistika: vymezení a teoretické základy. Praha: Vysoká škola ekonomická, 1994


Přidat komentář